
HOW WE TEACH
MINI PROJECTS
Mathematics is a challenging subject, and even those who enjoy it may find it too abstract at times.
Simply put, an abstraction is a summary of a concept. In math, this summary is often expressed using Greek symbols in the form of mathematical formulas. If you are the one who observed something special and summarizes it, the process can be quite intellectually satisfying. If you try to summarize something you observed but realized that others have observed more keenly or made better summaries than you, you can still learn a lot, and that is also quite satisfying. But if you are simply an audience member, listening to someone's summary about something you cannot relate to, then that kind of abstraction is what people tend to dread in math.
Condensed
The predicament of our math education is that we are attempting to condense thousands of years of mathematical development into just 12 years of lessons. As a result, we have to make a lot of summaries. But the more we summarize, the more abstract math becomes, making it increasingly challenging for students.
In order to fit so many years of discoveries into only 12 years, the school syllabus has no room for many actual mathematical activities that took place during math's development. In the classroom, students mostly see a summary of these activities, along with some weak attempts to explain their context.
In this article, we showcase how we reintroduce these mathematical activities back into our curriculum through the use of mini-projects. We will use trigonometry as an example, a topic that many students find either challenging and abstract or simple but tedious.
Modelling A Cube
A generation ago, calculators began to find their way into the math curriculum. But we believe that soon the use of computers will become as common as calculators in the classroom.
Computers open up many options in terms of what we can do in class. For example, students can learn about trigonometry by modelling a cube on a spreadsheet.
People who use spreadsheets know how we can record our data and turn it into a line graph. For example:

Because the positions of the eight corners of a cube can be represented by numbers, when we enter these numbers onto a spreadsheet, we can “draw” the cube on the screen. Then, by rapidly recalculating these numbers (using trigonometry) and refreshing the screen, we can create the illusion that a cube is rotating. Here is what a student did:
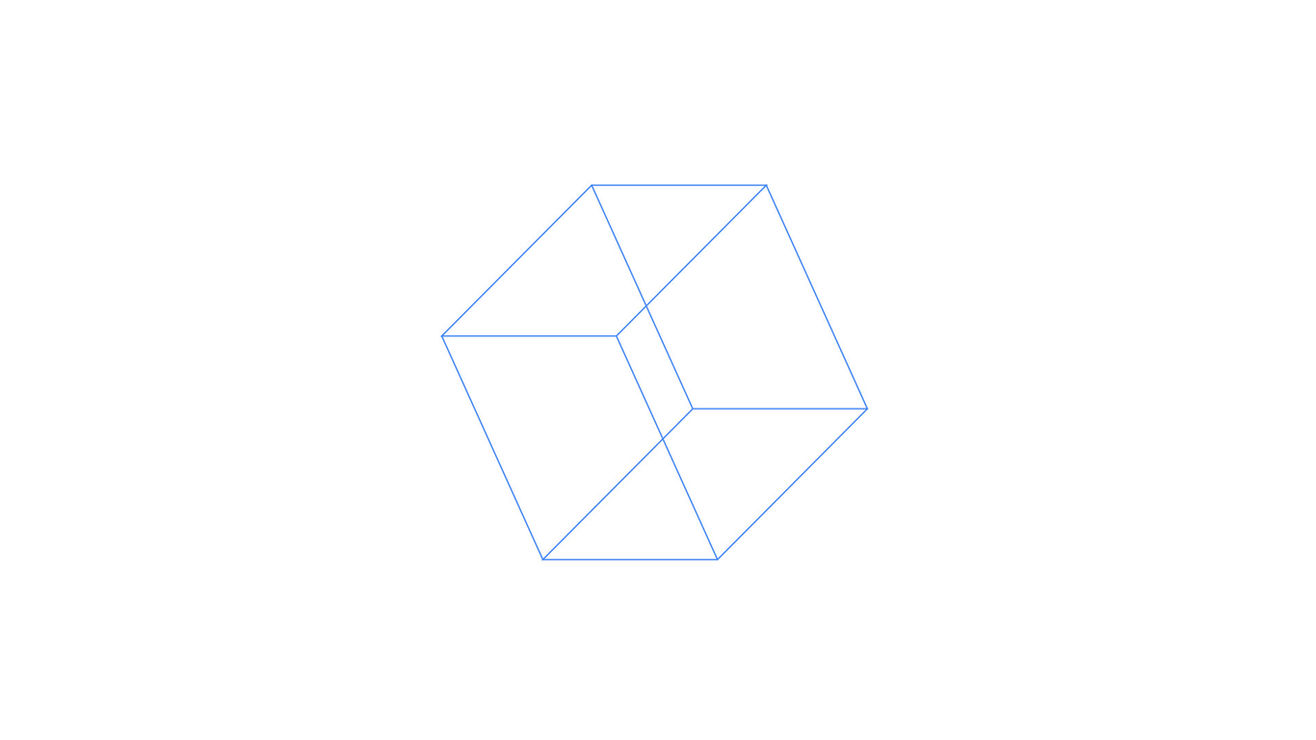
Students nowadays are exposed to the mesmerizing computer animations on their screens. But there is such a disconnect between school work and the actual world that it wouldn't occur to them it is possible to understand and create their own computer animation using just what they have learned in school.
People think we have to learn a lot of math before we can start using it in real applications. On the surface, that make sense because for example, it is more convenient if you gather all your ingredients first before you start cooking a dish. Otherwise, imagine the hassle if you only realize you are out of some essential ingredients while you are half-way cooking.
However, our math education can feel like a never-ending process of gathering ingredients. Every time we meet one teacher, we learn a few ingredients from them. We do not know what to do with these ingredients except there is an unspoken trust that a next teacher will come and show us how to turn those ingredients into a dish. But when you meet the next teacher, more often than not, the same thing happens - they teach you a few more ingredients, and leave it to the hypothetical next teacher to show you how to cook the dish.
In the end, most students spent years and years gathering ingredients without knowing what they are cooking, Many would not stick around long enough to ever find out.
While having a good grasp of the basic ingredients helps a lot in learning the applications, the truth is, not every ingredient is needed for every dish. With some ingenuity, we can cook something simple with just the ingredients we currently have. We think it is better to do that with students that as soon as possible.
For example, any student whom you would expect to do well in O-levels would be capable of completing our cube-modelling activity. It is still a challenging task. Students will have to develop grit and learn to make wider connections than what is required for the exam questions. But all the math required are already tested in O-levels. Instead of spending all their school years practicing exam questions, some students will be better engaged if they spend part of their time on these challenging but instructive activities.
But before you attempt to model a cube, there are simpler activities to hone your skills . We show some "simpler" examples next.
Ancient Methods, Modern Technology
In one activity, we task our students to calculate the distance between any two locations on Earth, given their longitude and latitude. Here is what a student did:
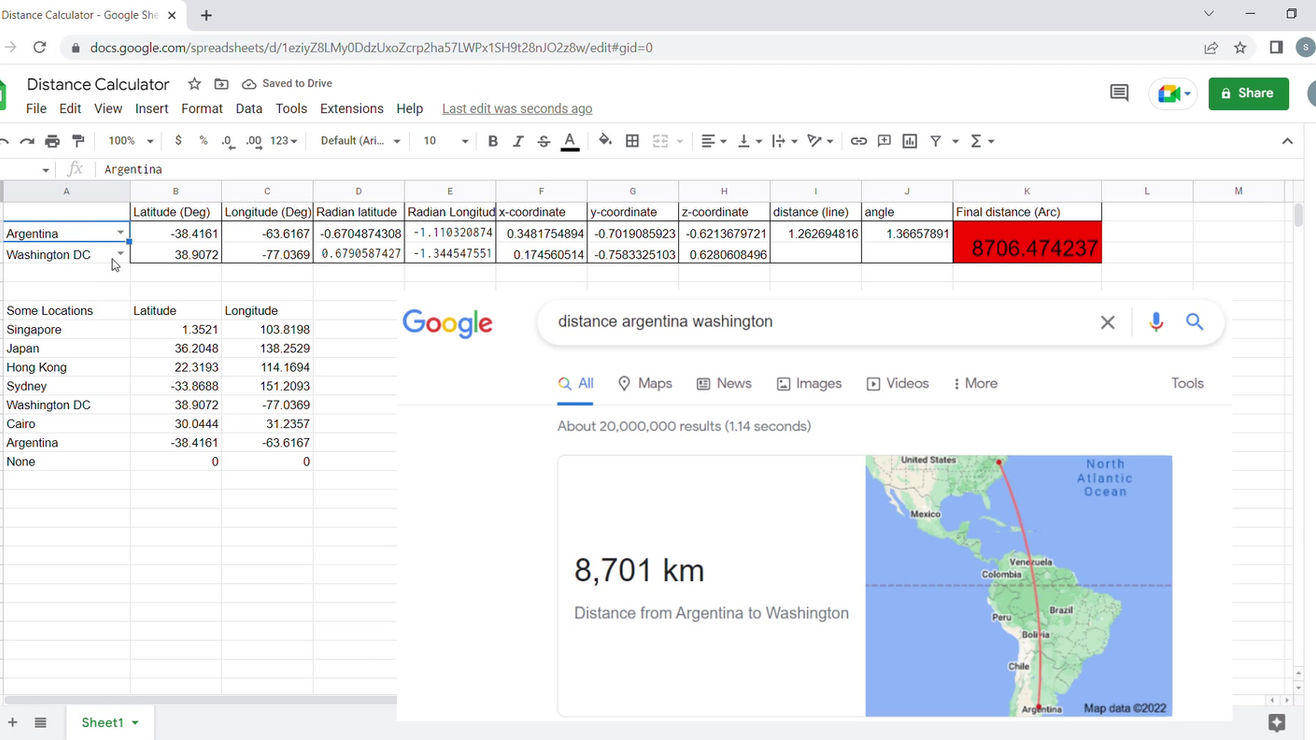
This mini project is part of a series of activities where we trace our ancestors' footsteps to figure out how big is the world, using just the limited knowledge they had. When laborious calculations are needed, we allow students to use the calculator or computer. Knowing how much calculations our ancestors had to perform manually in order to answer these questions, one has to admire their resolve and dedication. It is no wonder mathematicians were the ones who first imagined and went on to invent the calculator and computer.
Some of these ancient techniques are obsolete now, but some are timelesss and we are still learning them in school today. Regardless of whether they are obsolete or still in use, every activity is a case study of how someone made an insight to use math in ways never seen before by the people of their era.
We hope this juxtaposition of ancient methods and modern technology prompts our student to appreciate how far humanity has come and perhaps make them wonder what may lie in our future.
Origin Stories
Many people like a good origin story, as evidenced by the popularity of superhero origin stories in films. In math, there are also fascinating origin stories, such as the ones told in the National Geographic’s television series “Cosmos”.
There are dull ways to tell these origin stories. But there are also interesting ways. When told well, these stories make you care about what you are learning. When you care, you also become curious about the details. But very often, the medium through which these stories are wonderfully told is unable to include the details like the actual math involved in the events. So, as classroom teachers, the ball is in our court now to design activities that fill these gaps.
Descendants of Astronomers
We are descendants of astronomers. Our ancestors were farmers who relied on the changing seasons to determine when to plant and harvest crops. They realized that some stars return to the same position in the sky at regular intervals. So, they carefully observed the sky and made tables of these stars' positions, hoping to predict the change in seasons. One crucial achievement was their creation of the sine table, which allows them to make the right calculations.
In the next example, our students put themselves in the shoes of these ancient astronomers and attempt to build a sine table from scratch.
If you don't have time for this activity, you could have skipped it by just learning the list of formulas needed to build a sine table - which is basically how the school syllabus summarizes everything: they show you a bunch of formulas and demonstrate why the formulas are correct. You can still learn a lot by studying how to derive these formulas. But void of any context and purpose, these formulas become abstract.
Some people are fine with this level of abstraction and some are not. In any case, if you had tried to build a sine table, your mindset would be different because you are focusing on the problem of building a sine table instead of the tools which are the formulas. In the end, you still learn the formulas. But because of the process, the formulas become more relatable.
Interconnected Concepts
Math is not just a set of unrelated techniques labelled as different topics. Instead, it is a web of interconnections. As our ancestors continued on their quest to figure out the size of the world, new concepts, like functions, as shown in the next example, naturally emerge.
These mini projects often require knowledge from across different subjects like math, science, history, geography etc. In the beginning, many students were genuinely surprised and we often hear them making remarks like: is this math or science? Are we learning geography? Etc.
In the school where our timetable is organized based on subjects, these activities are uncommon because they often do not belong nicely to one single subject.
Lost Insight
People say that truth can be found in simplicity. But if that is true, why is math so complicated?
For example, why do we use "radians" in trigonometry instead of the "degrees" that we already knew and learned since primary school? Or why do we want the trigonometric ratios to be positive in one quadrant but negative in another? The typical lesson in school does not answer such questions.
We can believe that the people who put these schemes in place knew why they are useful or necessary. But as the school syllabus tries to summarize their work, we gradually lost their insight along the way. For some students, having to follow these schemes without knowing their motivation can be quite annoying. It is by re-experiencing their work ourselves, or a simplified version of it, that we understand the motivation behind these schemes.
When the scheme is simple, it is still fine. You can memorize them by rote using mnemonics like "soh-cah-toa" or "SATC" etc. But these schemes are going to pile on top of each other and become increasingly complicated later on.
The situation is almost the same for every topic that comes after trigonometry. That is why some students can follow the logic of math quite well up to a certain level and still be shocked when they saw what math has become at the next level.
In Closing
These mini projects are a kind of project-based learning. They are themed around actual activities which took place as math was being developed. In our view, the school syllabus often present only a summary of these events and as a result, made math too abstract and inaccessible to even the keen learners. Through the mini projects, we guide our students to think through the issues that triggered math to develop in the way it did and help them explore why the paradigms which we adopt today makes sense.
For students who did well in PSLE, it is relatively easy to stay ahead of syllabus in the first two years of secondary school. But because it doesn't take much time to present a summary, the math topics in school can and will eventually be taught at what appears to many as an increasingly rapid pace.
On the other hand, our mini projects will always require a lot more time than the school syllabus needs to summarize them. Hence, we always encourage our students to learn ahead so we have the time to learn through these activities. In fact, that is in our view, the most important benefit of learning ahead.
(The mini projects shown here are done by secondary 2 and 3 students.)