
HOW WE TEACH
BEFORE 15 YEARS OLD
YX was a secondary student who likes physics. When she was self-learning physics from the internet, she learned that the explanations in physics often involve advanced math concepts that she doesn't understand.
At first, she tried to ask her school teacher, but soon realized that her questions might have caused some inconvenience. Not only was she asking about topics beyond her current syllabus — like the vector product, which appears frequently in physics — but she also had doubts about fundamental concepts within the syllabus that a typical student would never ask. For example, why is the formula for a sphere’s volume “4/3πr³” and not something else?
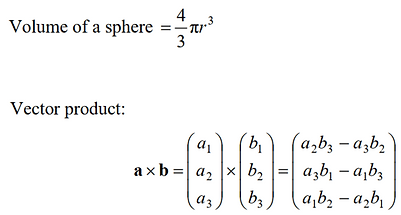
“My teacher just said if I want to understand everything, I should become a philosopher,” YX shared with us.
To support her interest, her mum approached us and asked if we could teach YX all the math she needed to understand physics. We thought this was an interesting challenge and agreed to help.
Richard Feynman - A Role Model for Curious Learners
Learning can be difficult even for those who are keen to learn. A student’s desire to learn does not automatically translate into their ability to learn — they still need guidance and inspiration from teachers and role models.
During one of our lessons, we asked YX if she knows who Richard Feynman was. She said yes and revealed that Feynman was her favourite physicist, someone she admired after reading his memoir:

Richard Feynman, a theoretical physicist who won the Nobel Prize, became renowned for his ability to explain difficult scientific concepts in an accessible way. At School of Mathcraft, we too admire Feynman for his charismatic teaching style and his unique views on education.
During WWII, Feynman was recruited into the Manhattan Project to help build the world’s first atomic bomb. This serves as a reminder that theoretical knowledge is not just an academic exercise — it also has the potential to impact the world in profound and sometimes controversial ways.
Euler's Formula: A Challenge for YX
Given our interest in understanding how students learn and their developmental stages, we were particularly intrigued by an anecdote about the teenage Richard Feynman: just before his 15th birthday, he could already understand Euler’s formula.
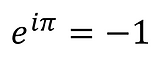
According to the story, young Feynman sketched out a proof of this baffling formula in his notebook and called it “the most remarkable formula” in math.
In fact, flipping through his later PhD thesis (figure below), one could easily spot many instances where Feynman applied his understanding of Euler’s formula to develop his theory on quantum mechanics. The thesis laid the foundation for the work that ultimately earned him the Nobel Prize.

We shared this story with YX and asked her how long she thought it might take her to understand Euler’s formula. Could “ordinary" students grasp it before the age of 15? We weren’t sure, but we thought it would be a fun experiment to see how “ordinary" students measure up against a future Nobel Prize laureate.
YX was interested to find out too. But we reminded her that this is no easy task. While many proofs of Euler’s formula are available online and in textbooks, most of them fail to make the formula intuitively clear. Given its complexity, there are also many hand-wavy proofs out there that gloss over important details.
Although we didn't know exactly how young Feynman proved Euler's formula, we believe — based on his later reputation as an excellent educator — that his proof was likely not just mathematically correct but also intuitively insightful.
With our shared admiration for him, we decided that YX should strive to find a proof that Feynman himself would have approved of.
Doing that is already challenging enough. But can she also do that before her 15th birthday?
The CIMB Problem
Leonard Euler, after whom Euler’s formula is named, lived in 18th-century Europe.

At that time, the banking system was still in its infancy, and mathematicians like Euler were instrumental in developing the mathematics that made modern banking possible.
To help YX grasp the intuition behind Euler’s formula, we started with a problem rooted in these early banking concepts.
The following was a task given to Nathaniel, a 7-year-old student in Primary One. His mother had just opened a savings account for him, and he mentioned that the annual interest rate was 1.5%. Sensing a teachable moment, we asked him to figure out how much the bank should give him every month. Since the bank in question was CIMB, we call it the “CIMB Problem”. This was his solution:
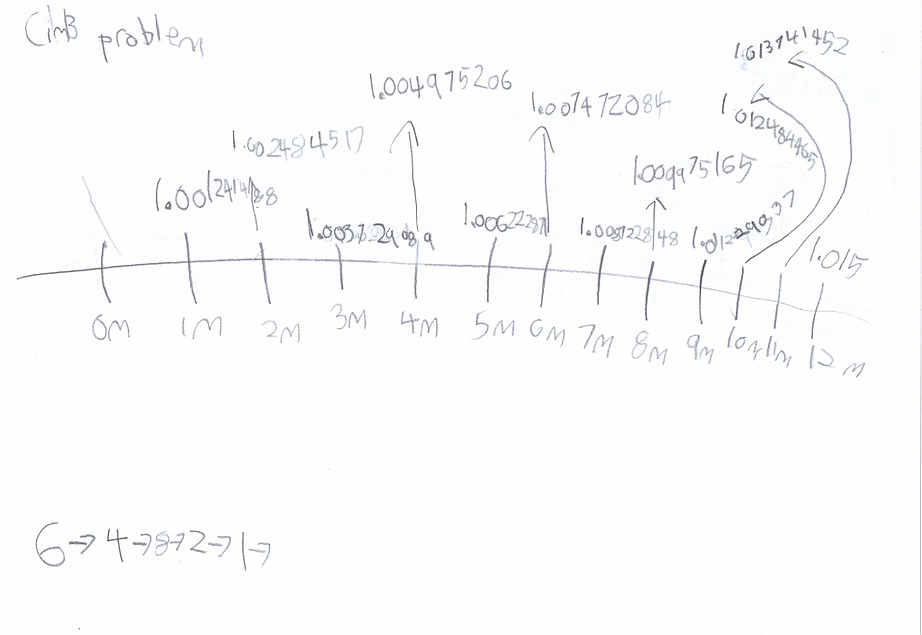
It took Nathaniel about six lessons to solve this problem because it was very challenging for him. Throughout the first five lessons, there were many moments when we saw how he struggled and secretly regretted giving him this problem, wondering if we had overestimated his ability. But on the sixth lesson, something clicked, and Nathaniel suddenly understood what he needed to do. We captured that moment on video:
Imaginative Play
After understanding the concept, Nathaniel went further and calculated how much interest his dad’s bank should pay every month at a higher interest rate (4% annual interest this time):
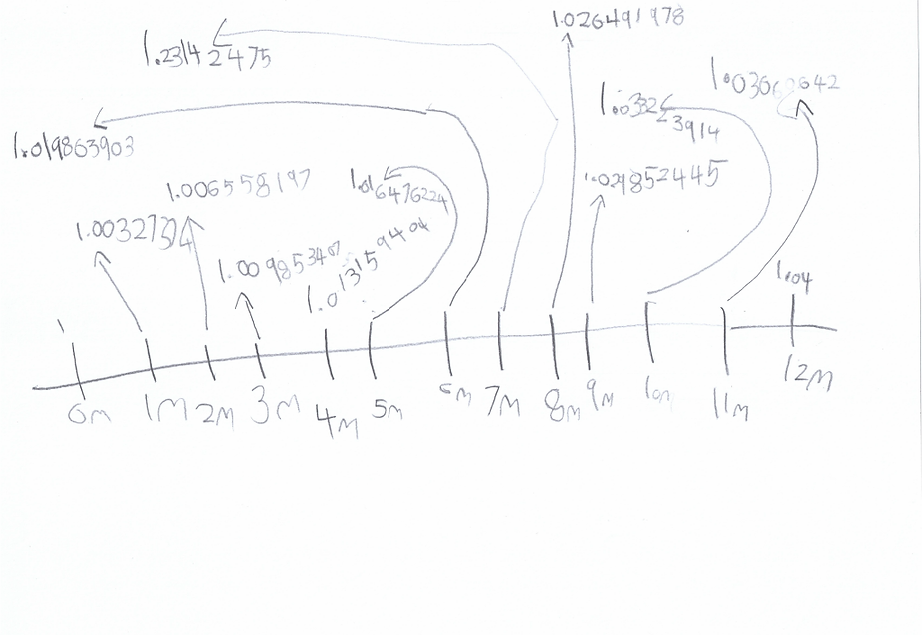
Here is a fun clip of Nathaniel working that out:
Did you catch how he “apologized” to the square-root? He was talking to these mathematical operations like how children talk to their toys when playing!
One, Two, Three
Officially, we only teach students aged 8 and above. But we realized Nathaniel’s case was special, and we could learn a lot from teaching him.
Nathaniel’s sense of numbers developed very early. He was 6 years old when we first met him, and on the first day he came, he told us that his house was 26 minutes away from our centre. That comment was highly unusual for a child his age and hinted that numbers were already a natural part of his perception.
In fact, his mum mentioned that his first words were “one, two, three” — but this was partly because he also had a delayed speech development: he started speaking late, and by the time he began talking, he could already understand numbers.
Rainbow Colours
However, math is more than just a good sense of numbers. It also involves a blend of abilities: logic, critical thinking, abstract thinking, problem-solving, procedural skills, disposition, metacognition, and more.
For most people, these abilities develop in sync. As a result, math is rarely seen as a multi-faceted activity. However, just as white light is composed of different colours, Nathaniel’s rare asynchronous development — where his number sense advanced early, while his speech delay may have affected the growth of other cognitive skills — allows us to witness the “rainbow colours” of the brain in action.

Teaching Nathaniel in those early years made us realise our worksheets demanded too much verbal logic and were unsuitable for him. Hence, we often designed number-related tasks to let him explore on blank sheets of paper.
For example, this is something he did before the “CIMB Problem”:

Great activity for kids who love numbers. We did these over a few lessons.

We solve it by listing all possible ways to sum to 15 -- an idea a P2 boy taught us many years ago!
Eventually, Nathaniel understood 90% of why the method (to solve odd-sided magic squares) work. We think that is good enough for him. So, we ended this activity.

Great activity for kids who love numbers. We did these over a few lessons.
Analogy versus First Principles
Euler’s formula is often baffling to those who do not understand exponents well.
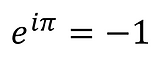
Even though exponents are considered one of the easiest topics in math curricula, they only appear that way because in school, exponents are taught through analogy. However, when you approach the topic from first principles — as Nathaniel did when solving the “CIMB Problem” — you begin to realise how much deeper the concepts truly are, especially when the analogy breaks down.
Thus, the first thing we did was help YX demystify exponents. Below are some of Nathaniel’s notes, illustrating how one can learn about exponents (and logarithms) from first principles:
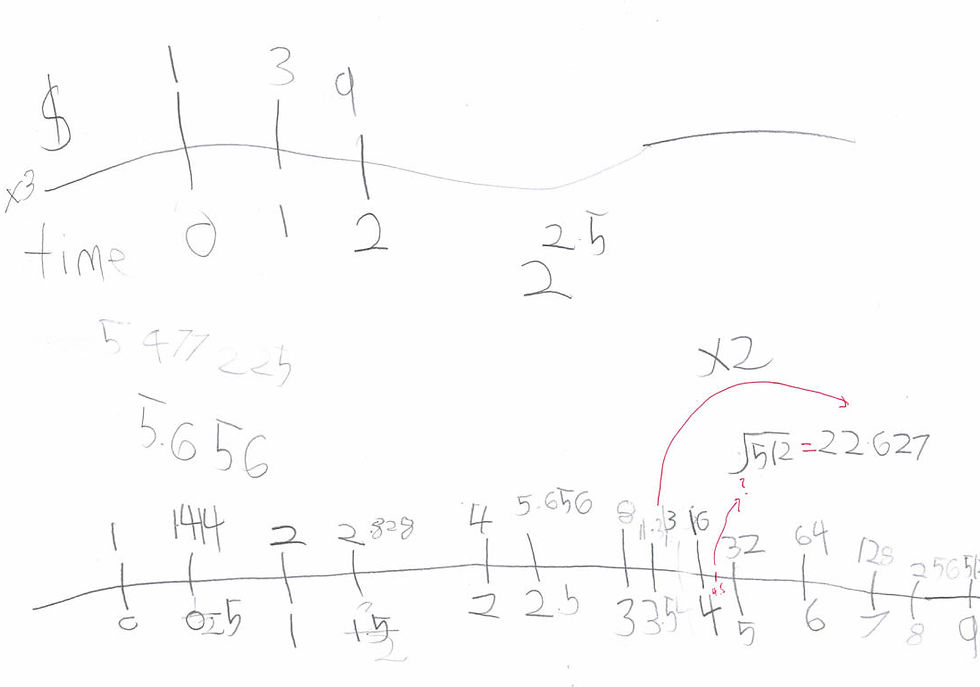
If the bank doubles your money (starting from $1) every year, how much should you get in half a year? Every student we asked said $1.5, but that is the wrong answer. The banks would lose money if they do that.
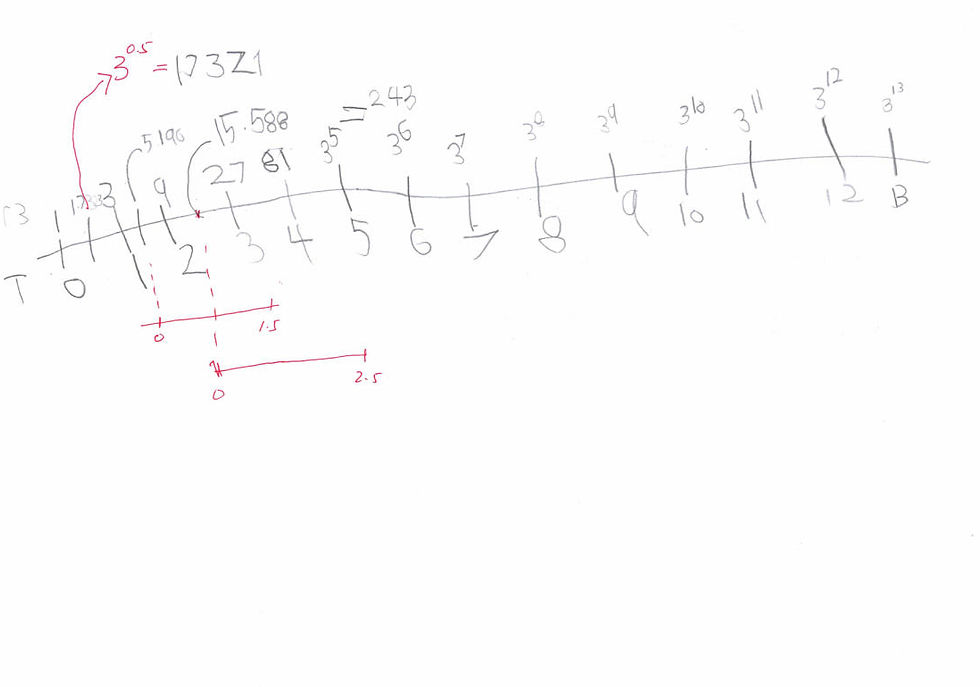
What if the bank triples your money every year? We asked Nathaniel's parents to buy him a scientific calculator. At this point, he only uses the 4 operators: +, -, x, /. Slowly, we will "unlock" other buttons.
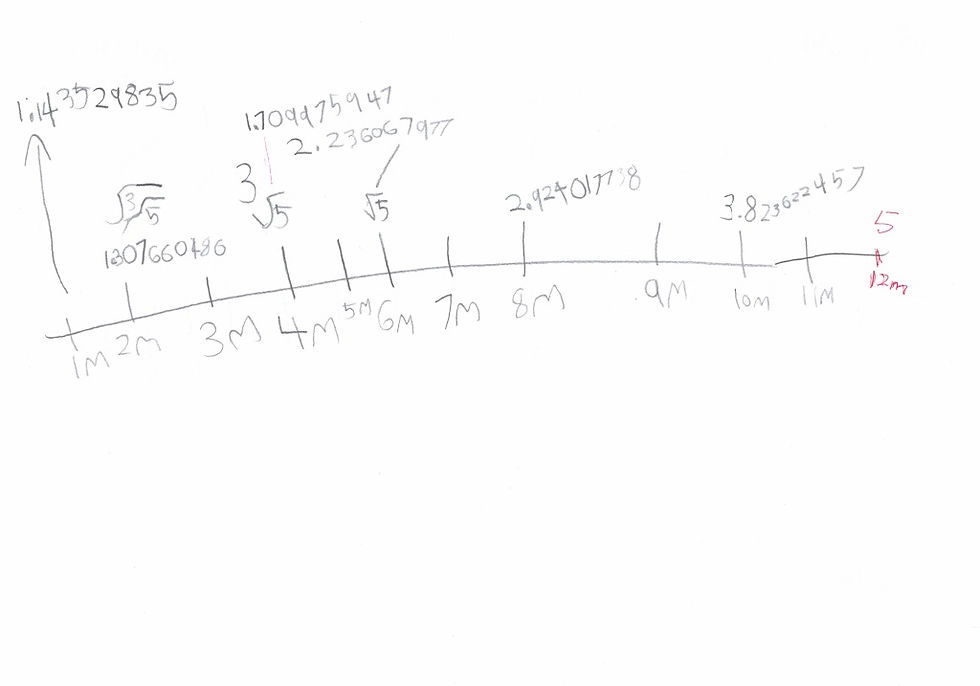
One final practice before solving the actual CIMB Problem.

If the bank doubles your money (starting from $1) every year, how much should you get in half a year? Every student we asked said $1.5, but that is the wrong answer. The banks would lose money if they do that.
Off by 1 Cent
When things got tough for Nathaniel, we motivated him by suggesting he should check whether CIMB had given him the correct amount of interest. Somehow, this appealed to his love of numbers and tickled his sense of fun:
Nathaniel: What if they are wrong?
Teacher: Then you can tell them.
Nathaniel: What if they don’t believe me?
Teacher: Then you’ll explain to them the right way to calculate it.
Nathaniel: What if they still don’t believe?
Teacher: …
With that motivation, he persevered and eventually solved the problem. When he checked his bank statement, he discovered that on 30 April, CIMB had given him 1 cent less than what he had calculated!
.jpg)
Did CIMB make a mistake? After further investigation, we realized the discrepancy arose because we had assumed each month was equally long, while CIMB calculated the interest based on the exact number of days in each month. Unfortunately, Nathaniel was too young to fully explore and resolve this discrepancy.
However, minor discrepancies can sometimes lead to significant insights. If Nathaniel had continued calculating the interest by day, or by increasingly smaller intervals — hours, minutes, seconds, and so on — he would eventually encounter a mysterious number known as Euler’s constant:

But to delve deeper, we would need help from someone older than Nathaniel.
Coding
Theo, a 9-year-old student, already knew how to code in Python. We explained to him what YX, Nathaniel and other students (in the rest of this article) were working on, and told him we needed his help to fill a gap in their work.
Within one week, Theo had already figured out the abstract relationships in the numbers that Nathaniel calculated and expressed them using mathematical notations:
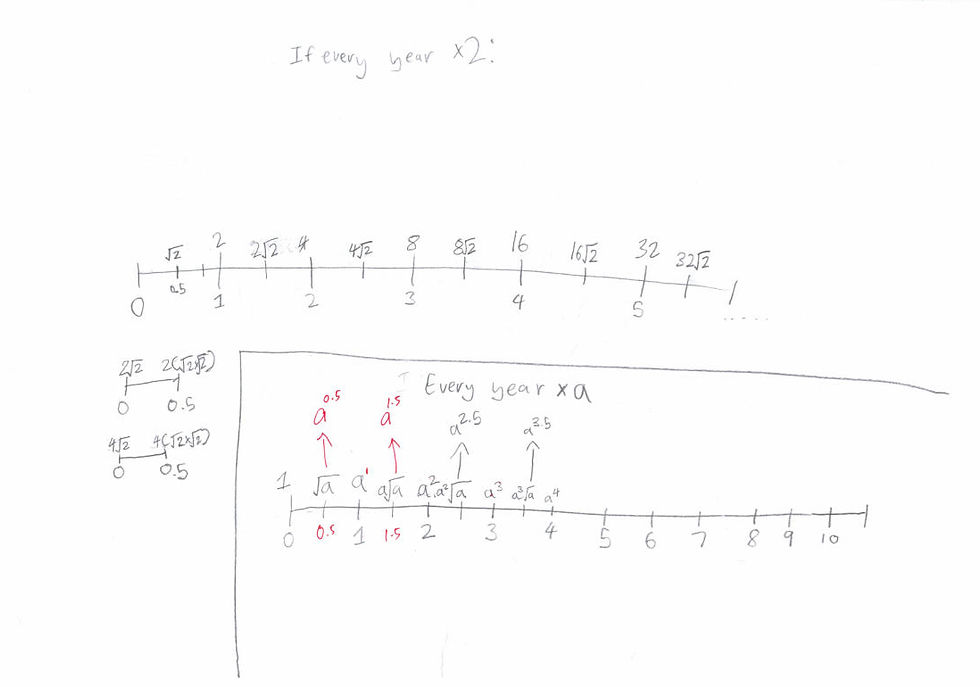
At the age of 9, Theo can already transition from concrete to abstract quite comfortably.
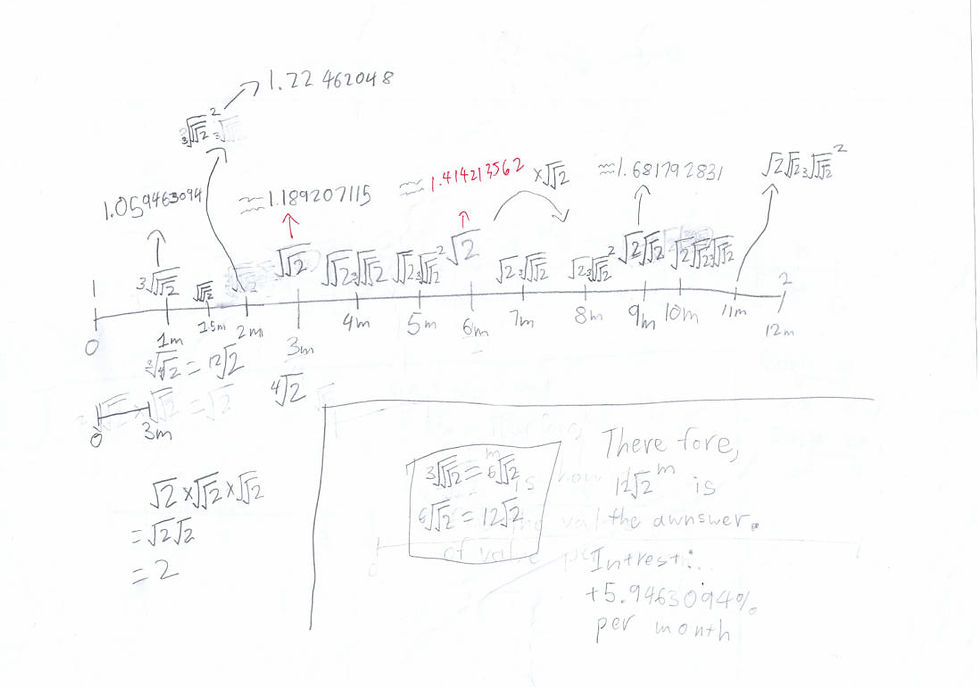
The eraser marks show he had changed his mind many times in the process.

He gave an example of how to apply his method.

At the age of 9, Theo can already transition from concrete to abstract quite comfortably.
Rather than using paper and a calculator like Nathaniel, we asked Theo to write some Python programs to automate the process. We hosted his code on Google Colab and shared some of his learning journey there:
Off by 1 Cent, Again!
In the end, Theo's program showed that on 30 April, the amount of interest CIMB had given Nathaniel was indeed wrong, and was off by 1 cent. But this time, based on his calculation, CIMB had given 1 cent more than the correct amount!
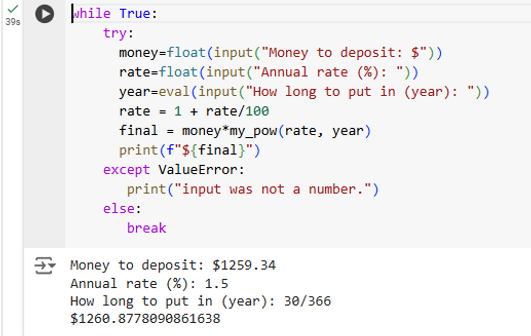
It turns out that banks always give people slightly more interest than they technically should.
While Theo’s program can calculate the mathematically correct amount of interest, this method is too cumbersome for practical use. So, banks use a simplified formula — the “Compound Interest Formula” taught in school — to calculate interest:
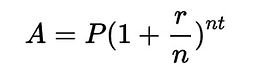
Bernoulli's Inequality
What’s mathematically intriguing is how banks ensure that this formula never yields an interest lower than the correct amount, which is crucial for avoiding accusations of fraud. On the other hand, how can they guarantee that the formula’s results stay close to the actual amount? That is equally important, as banks don’t want to lose too much money.
Nathaniel and Theo understood these concerns, though they lacked the math skills to verify this hypothesis. So, we suggested to YX that this might relate to Bernoulli’s Inequality and encouraged her to work out the details. Later, she turned this into a research project for school. However, that was after her 15th birthday, so we won’t include it here.
Numbers, Symbols, Formulae
So far, we’ve shown how numbers turned into symbols and, eventually, into formulae. But that doesn’t mean numbers lose their importance. Like a finger pointing toward the moon, formulae are simply tools that summarize patterns within numbers.
The first person to do something like Nathaniel and Theo — John Napier — lived in the 16th century. Without a calculator or computer, he spent twenty years of his life compiling tables of these numbers so others (mainly astronomers) could use them without recalculating.
Theo’s program was based on an algorithm from Euler’s work, which summarized what his contemporaries knew about calculating these numbers:

Euler's "Introduction to Analysis of Infinite"

Euler's "Introduction to Analysis of Infinite"

Euler's "Introduction to Analysis of Infinite"
But Euler, ever the prolific mathematician, went on to derive a formula to replace that algorithm.
Euler’s constant
XT, who is the same age as YX, used Euler’s ideas to dig deeper into Nathaniel’s CIMB Problem. In her work below, she revealed Euler’s constant “e” and derived a formula to replace Theo’s algorithm:

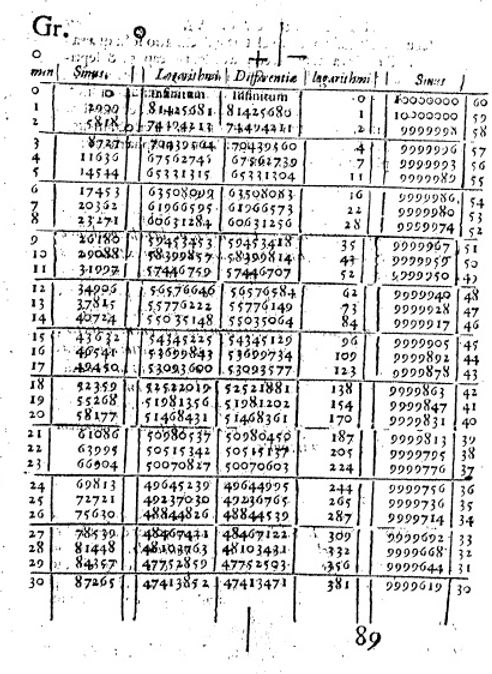
This represents a significant jump in abstraction from Theo’s work. To reach this level and beyond, our students need strong foundations in Euclidean geometry, algebra and trigonometry. In particular, we studied how Archimedes calculated Pi and how Ptolemy constructed the Sine table — both essential to understanding Euler’s formula.
Below is XT calculating Pi to 14 decimal places:

Below is another student, Ethan, constructing a table of Sine values:
Calculus
While calculus isn’t necessary to derive Euler’s formula, it allows us to verify the formula from different perspectives and explore its potential applications.
The typical textbook proof of Euler's formula relies on calculus. However, we find this approach unsatisfying because it doesn't give meaningful insight into the formula. At best, it shows that the formula isn't wrong. We are searching for a proof that reveals why the formula is right. After all, "not wrong" isn't quite the same as "right".
By age 15, advanced students like XT would have completed several mini-projects on calculus. For example, here is XT using calculus to prove that circular motion is caused by a centripetal force:

Finally
Finally, equipped with these prerequisites, YX derived Euler’s formula:

On the top right, she had a sketch of the standard proof in textbooks. The rest is based on how Euler derived it. His idea was truly breathtaking. But we won't elaborate here.
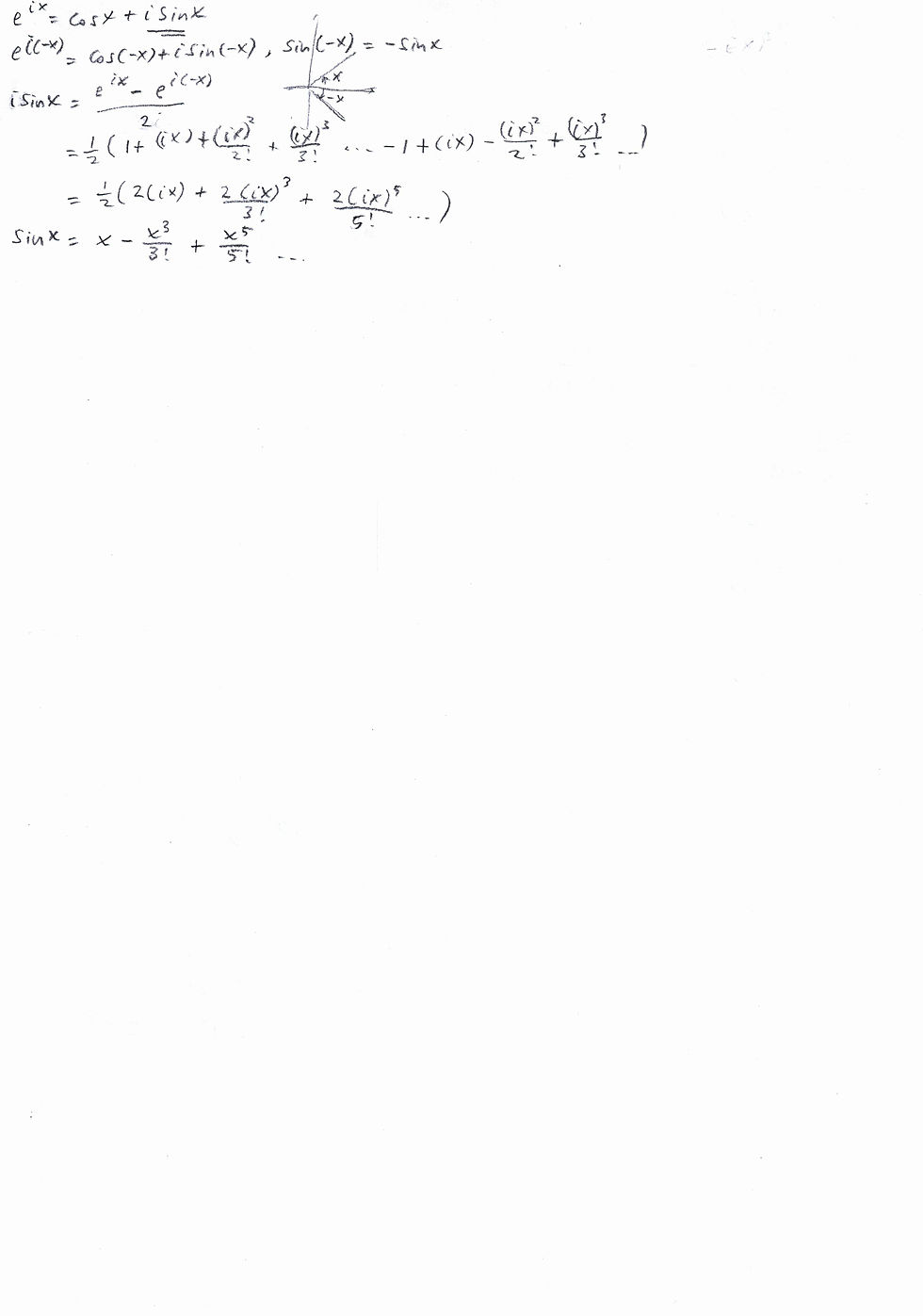

On the top right, she had a sketch of the standard proof in textbooks. The rest is based on how Euler derived it. His idea was truly breathtaking. But we won't elaborate here.
And yes, she did this before her 15th birthday!
Motivation
When we mentioned to YX how Richard Feynman understood Euler’s formula before he turned 15 and suggested it might be fun for her to try, it was more of a probe — a way for us, as teachers, to see what might spark her interest.
YX wasn’t the only student to whom we’d made this suggestion, but she was the one who took it seriously.
Our lessons are flexible enough to adapt to students’ evolving needs (within certain parameters). Yet for this same reason, there are many scenarios where we could easily have been sidetracked by other objectives.
When YX was in primary school, our focus was on preparing her for PSLE. Although she wasn’t progressing quickly enough to compete in math competitions, we still consistently gave her competition problems to solve at her own pace. She never shied away from these challenges and developed a strong foundation in problem-solving.
In secondary two, we helped her prepare for her first math competition — the Australian Mathematics Competition — and she won a High Distinction. Buoyed by this success, she moved on to prepare for her next competition. However, midway through, she told us she felt bored and wanted to return to learning Euler’s formula. That was when we knew it meant something special to her.
This reminds us of something Richard Feynman once said in an interview. We only agree with half of what he said, but we’ll leave you to ponder it.
Application
When we told Charles about YX’s work, he wanted to challenge himself as well.
Although Charles didn’t have time to complete every mini-project that YX did, he submitted an excellent presentation of the proof of Euler’s formula:

Like YX, Charles also asked if Euler’s formula had any practical applications. We showed him how Euler’s formula provides an alternate proof that circular motion results from a centripetal force:

Epilogue
After achieving what we set out to do, we became curious about young Feynman’s own proof. Eventually, we found it:
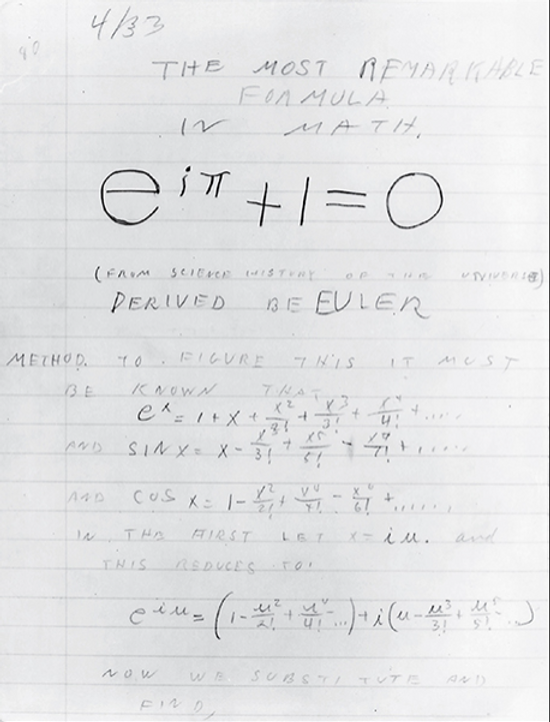
When YX saw it, she was speechless — it was just the typical textbook proof!
It turns out we may have set our bar too high and gone on a bit of a wild goose chase.
But every student — from Nathaniel to YX — learned a great deal along the way. We hope these stories about how they learn can become inspiration for others.
(Every piece showcased in this article was completed before each student turned 15.)